四种相似度计算方式概述
(一)欧几里得距离(L2)
原理:测量两点间直线距离,距离越小越相似。

公式:L2(X,Y)=∑i=1n(xi−yi)2。

示例:向量 A [1,2,3] 与向量 B [4,5,6] 的 L2 距离约为 5.2。
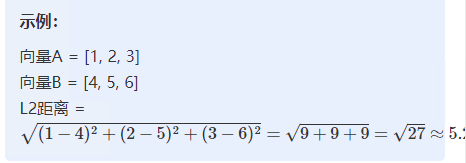
适用场景:图像检索、人脸识别、向量模长有意义的场景。
(二)内积(IP)
原理:测量向量方向相似度和大小乘积,值越大越相似。

公式:IP(X,Y)=∑i=1nxi⋅yi。

示例:向量 A [1,2,3] 与向量 B [4,5,6] 的内积为 32。

适用场景:推荐系统、向量已归一化、需考虑向量大小和方向的场景。
(三)余弦相似度(Cosine)
原理:测量向量夹角,忽略大小,关注方向,值越接近 1 越相似。
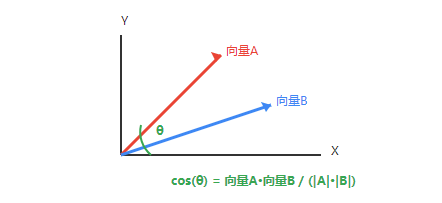
公式:Cosine(X,Y)=∣∣X∣∣⋅∣∣Y∣∣X⋅Y。
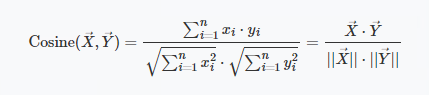
示例:向量 A [1,2,3] 与向量 B [4,5,6] 的余弦相似度约为 0.975。

适用场景:文本相似度比较、仅关心方向的场景、自然语言处理。
(四)汉明距离(Hamming)
原理:计算等长字符串或二进制串对应位置不同的数量,距离越小越相似。

公式:Hamming(X,Y)=∑i=1n[xi=yi]。

示例:向量 A [1,0,1,0,1] 与向量 B [1,1,0,0,0] 的汉明距离为 3。

适用场景:错误检测和纠正、生物信息学、二进制特征比较、图像哈希比较。
四种度量类型对比
度量类型选择建议
欧几里得距离(L2):适用于向量绝对大小有意义的场景,如图像特征、物体坐标等。
内积(IP):适用于向量已归一化或需考虑向量大小和方向的场景。
余弦相似度(Cosine):适用于仅关心方向的场景,如文本向量、语义相似度等。
汉明距离(Hamming):适用于处理二进制特征或哈希值的场景。
注意事项
在 Milvus 中创建索引时,必须指定合适的metric_type参数,该参数将决定向量相似度的计算方式,比如这里用的是余弦相似度: